تعريف

ينص قانون كيرشوف الأول علي : في أي شبكة من الموصلات يكون المجموع الجبري للتيارات عند نقطة تجميع Junction  مساويا للصفر. و يعني ذلك أن مجموع التيارات الداخلة علي النقطة مساويا لمجموع التيارات الخارجة، وهذا صحيح لعدم وجود تخزين أو  نقص عند هذه النقطة.  والشكل (1) يوضح النقطة A ومجموعة من التيارات المختلفة والمعادلات الخاصة بالتيارات.

Assuming the incoming currents to be positive and the outgoing currents negative, we have

   I₁ + (-I₂) + (-I₃) + I₄ + (-I₅) = 0

or I₁ + I₄ - I₂ - I₃ - I₅  = 0

or I₁ + I₄ = I₂ + I₃ + I₅

or Incoming Current = Outgoing Current

We can express the above conclusion thus

S I = 0          at any junction

و ينص قانون كيرشوف الثاني علي : المجموع الجبري لحاصل ضرب التيار في المقاومة في مسار مغلق closed mech زائد المجموع الجبري للقوة الدافعة الكهربية في هذا المسار يساوي الصفر . والعلاقة التالية تلخص هذا القانون:

S IR + S  e.m.f. = 0          round mesh

ولتحديد الإشارة يتم إتباع التالي:

1- القوة الدافعة المتزايدة : +

2- القوة الدافعة المتناقصة : -

3- مع اتجاه التيار في المقاومة : -

4- عكس اتجاه التيار في المقاومة : +

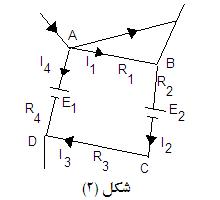
ويوضح الشكل (2) مثالا لتطبيق إشارة الجهد الكهربي داخل حلقة مغلقة في اتجاه  ABCD.

I₁R₁ is –ve  (fall in potential)

I₂R₂ is –ve  (fall in potential)

1₃R₃ is –ve (fall in potential)

I₄R₄ is +ve  (rise in potential)

E₂    is –ve  (fall in potential)

E₁    is +ve  (rise in potential)

و بتطبيق قانون كيرشوف الثاني:

-I₁R₁ - I₂R₂ - 1₃R₃ + I₄R₄ - E₂ + E₁ = 0

I₁R₁ + I₂R₂ + 1₃R₃ - I₄R_{4 =} E₂ - E₁

اتجاه التيار

عند تطبيق قانونا كيرشوف للدوائر الكهربية يتم فرض اتجاه التيار مع الساعة أو عكس الساعة و في حالة أن يكون الفرض معاكسا للواقع تنتج اشارة سالبة للتيار. و يتم استخدام الفرض خلال كل المعادلات. و يمكن تطبيق قانونا كيرشوف لدوائر التيار المستمر و التيار المتردد. و في حالة التيار المتردد يلزم اعتبار الجهد علي المكثف و المحاثة.

طريقة ماكسويل لحلقة التيار Current Loop

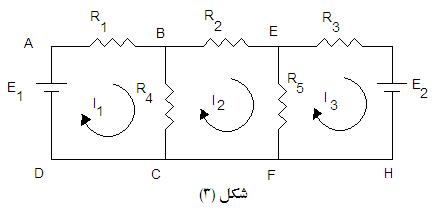
في هذه الطريقة يتم اعتبار التيار في شكل حلقة loop  و ليس في شكل فرع branch كما في حالة قانون كيرشوف علي أن يتم استخدام نفس طريقة تحديد الاشارات . و يوضح الشكل (3) مثالا لهذه الطريقة. و يمكن استنتاج تيار الفرع من تيارات الحلقة  كالتالي :

التيار في المقاومة  R₄  يساوي :  (I₁ - I₂)

التيار في المقاومة  R₅  يساوي :  (I₂ – I₃)

و القاعدة العامة لحساب التيار داخل الحلقة أن يتم طرح تيار الحلقة الأخري المعاكس. و فيما يلي معادلات الجهد الكهربي للحلقة في المثال الموضح في الشكل (3).

Loop ABCDA:

Starting from point A, we have

- I₁ R₁ – R₄ (I₁ – I₂) + E₁ = 0

Simplifying it further, we have

I1 (R₁ + R₄) - I₂ R₄ = E₁                               …(i)

Loop BEFCB:

Starting from point B, we have

- I₂ R₂ – R₅ (I₂ – I₃) – R₄ (I₂ – I₁) = 0

Or   I₁ R₄ – I₂ (R₂+ R₄+ R₅) + I₃ R₅ = 0             …(ii)

Loop EGHFE:

Starting from point E, we get

- I₃ R₃ – E₂ – R₅ (I₃ - I₂) = 0

or    I₂ R₅ – I₃ (R₃ + R₅) = E₂                            …(iii)

و يتم حساب التيارات الثلاثة من حل المعادلات الثلاثة.

نظرية سفننس Thevenin’s Theorem

تنص هذه النظرية انه لأي شبكة كهربية يمكن حساب مكافئ كهربي بين طرفين يتكون من مصدر  قوة دافعة كهربية (مصدر سفننس ) ومتصل علي التوالي بممانعة كهربية أو بمقاومة في حالة شبكات المقاومات. ويتم حساب المصدر الكهربي والمقاومة الداخلية طبقا للتالي :

1-  قيمة جهد المصدر تساوي جهد الدائرة المفتوحة بين الطرفين

2-  قيمة المقاومة الداخلية تساوي مكافئ المقاومة المحسوبة بين الطرفين مع عدم اعتبار  مصادر الجهد . 

و تستخدم هذه الطريق لحساب التيارات في الدوائر المعقدة. و يوضح الشكل (4) مثالا لاستخدام هذه الطريقة. والمطلوب حساب التيار في المقاومة R₃  في الشكل (4-أ) ولذا يتم فتح الدائرة بين الطرفين  A-B . ويلي ذلك حساب الجهد الكهربي للدائرة المفتوحة بين الطرفين A-B في الشكل (4-ب) طبقا للتالي :

V=drop across R₂ = I R₂

Where I is the circuit current when A and B are open.

I = E / (R₁+ R₂+r)

Then    V= I R₂= E R₂ / (R₁+ R₂+r)

ويلي ذلك حساب مكافئ المقاومة بين A-B بعد استبعاد المصدر E ومع اعتبار المقاومة الداخلية r، و في هذه الحالة تكون الدائرة عبارة عن مقاومتان علي التوازي كما في الشكل (5-أ).  و المقاومة المكافئة يتم حسابها طبقا للتالي:

R = R₂ (R₁ + r)/ [R₂ +(R1 + r)]

وبالتالي يمكن تحويل الشبكة بين الطرفين A-B إلي مصدر سفننس V و المقاومة الداخلية R كما في الشكل (5-ب). ويمكن حساب التيار في المقاومة R₃ بعد توصيلها بين الطرفين A-B كالتالي:

I = V / (R + R₃)

 التحويل بين دلتا الي نجمة

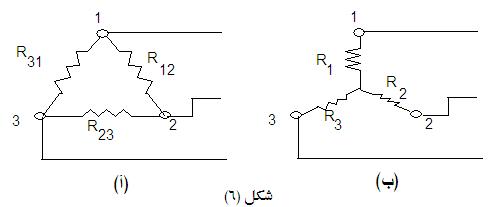
يتم استخدام هذه الطريقة في حل الشبكات المعقدة عن الطريق التحويل من دلتا الي نجمة أو العكس. و  يوضح الشكل (6-أ) دائرة في شكل دلتا و تحويلها الي نجمة في الشكل (6-ب). و يمكن استنتاج العلاقة عن طريق تساوي الجهد الكهربي لكل من الدائرتين و نحصل علي العلاقة التالية بين مقاومات الدلتا و مكافئها من النجمة.

R₁ =    R₁₂ R₃₁ /(R₁₂ + R₂₃ + R₃₁)

R₂ =    R₂₃ R_{1 2} /(R₁₂ + R₂₃ + R₃₁)

And   R₃ =       R₃₁ R₂₃ /( R₁₂ + R₂₃ + R₃₁)

كما نحصل علي العلاقة التالية بين مقاومات النجمة و مكافئها من الدلتا.

R₁₂ = (R₁ R₂ + R₂R₃+ R₃R₁)/ R₃= R₁ + R₂+ R₁ R₂ / R₃

R₂₃ = (R₁ R₂ + R₂R₃+ R₃R₁)/ R₁= R₂ + R₃+ R₂ R₃ / R₁

R₃₁ = (R₁ R₂ + R₂R₃+ R₃R₁)/ R₂= R₁ + R₃+ R₁ R₃ / R₂

يمكن استخدامه لتحديد مكافئ للدوائر الكهربية و لكن في صورة مصدر تيار مع مقاومة علي التوازي. ويمكن استنتاجه من مكافئ سفننس كالتالي :

I = V_th / R_th

و يوضح الشكل (7) التناظر بين مكافئ سفننس و مكافئ نورتن.